NAND2Tetris

Part 1

Table of contents

1. Boolean Logic
   1. Boolean Identities
2. Boolean Function Synthesis
3. Logic Gates
4. Hardware Description Language
5. Hardware Simulation
6. Boolean Arithmetic
7. Week 3: Memory
8. Week 4: Hack Programming

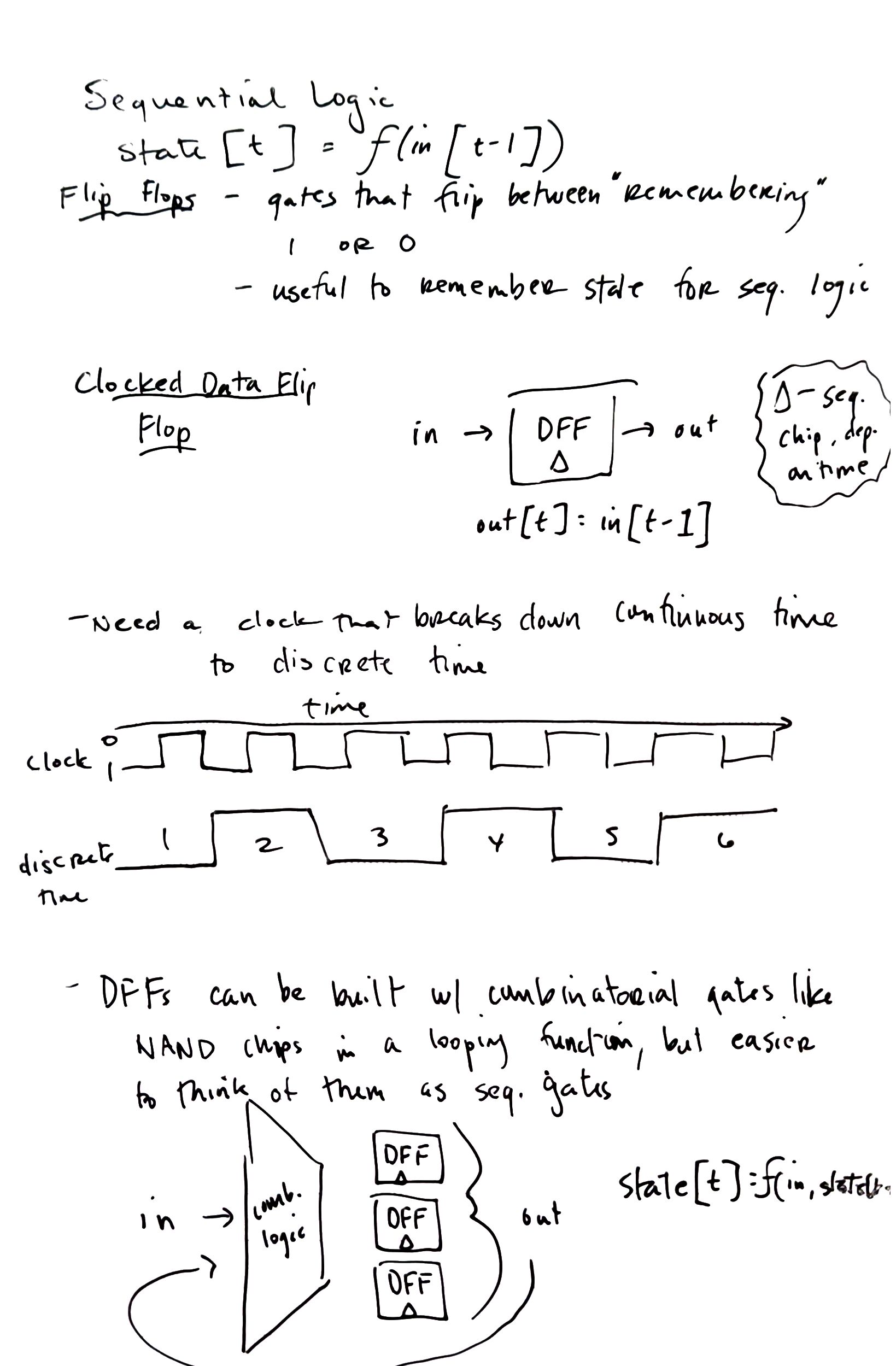
Boolean Logic

• truth table – gives all possible outputs of inputs, another way of representing boolean function
• unary operation – only takes single input

Boolean Identities

commutative laws (x AND y) = (y AND x) (x OR y) = (y OR x)

associative law (x AND (y AND z)) = ((x AND y) AND z) (x OR (y OR z)) = ((x OR y) OR z)

distributive law (x AND (y OR z)) = (x AND y) OR (x AND z) (x OR (y AND z)) = (x OR y) AND (x OR z)

de morgan laws NOT(x AND y) = NOT(x) OR NOT(y) NOT(x OR y) = NOT(x) AND NOT(y)

Boolean Function Synthesis

• any boolean function can be represented using an expression containing NAND operations (x NAND y) = NOT(x AND y)

Logic Gates

• technique for implementing boolean functions using logic gates
• elementary (NAND, AND, OR, NOT, etc.)
• composite (MUX, ADDER, etc.)

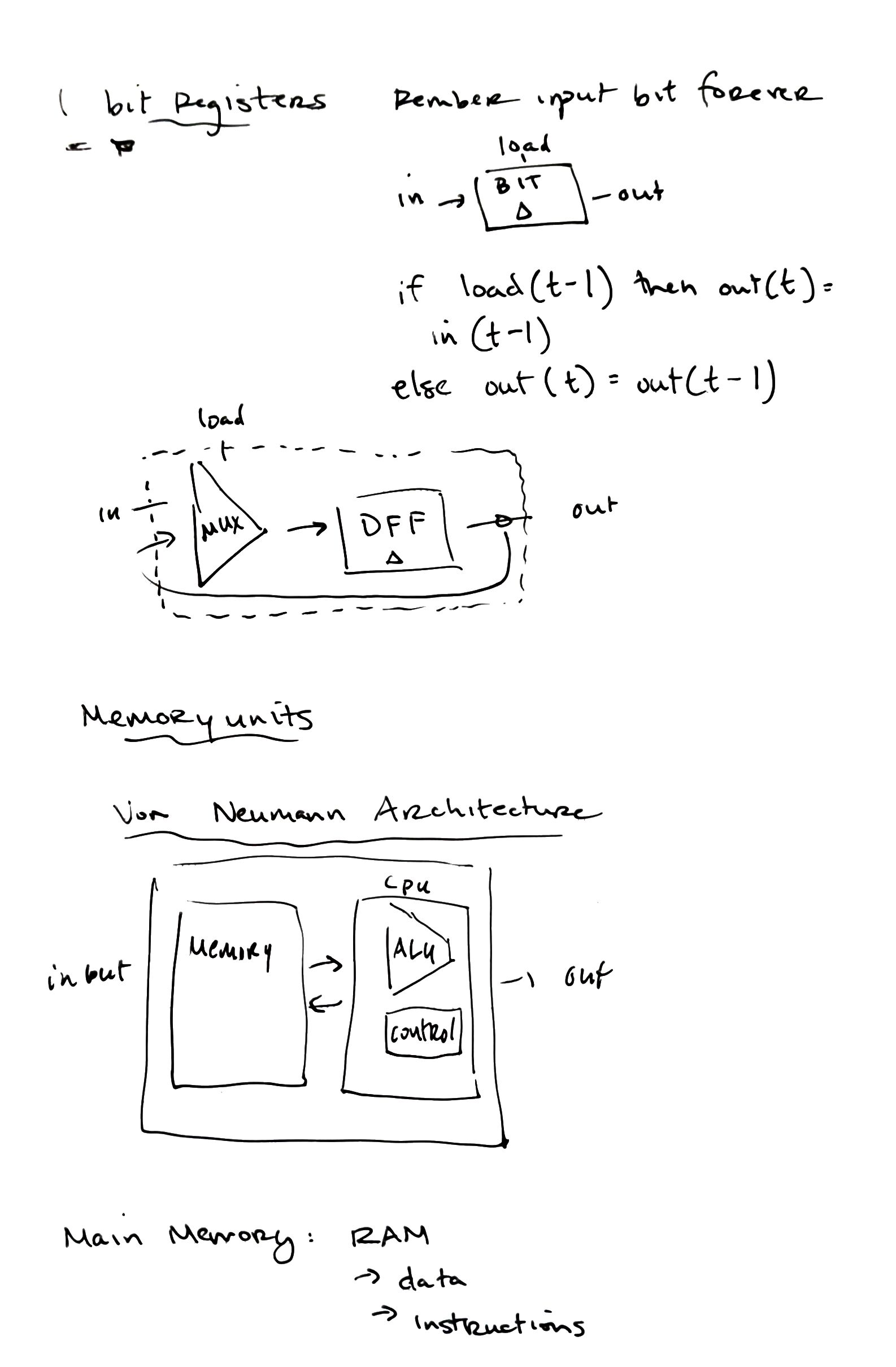
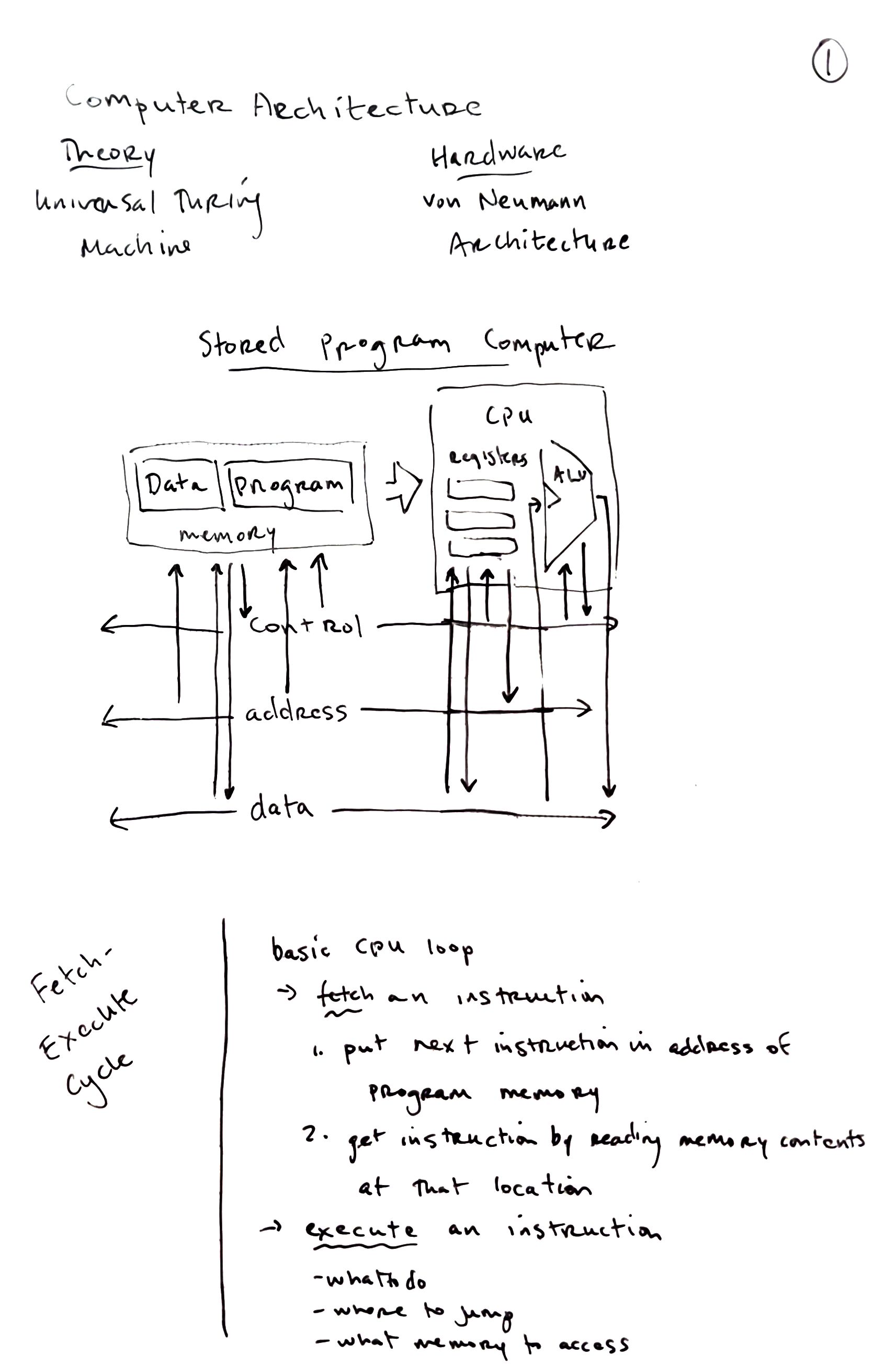
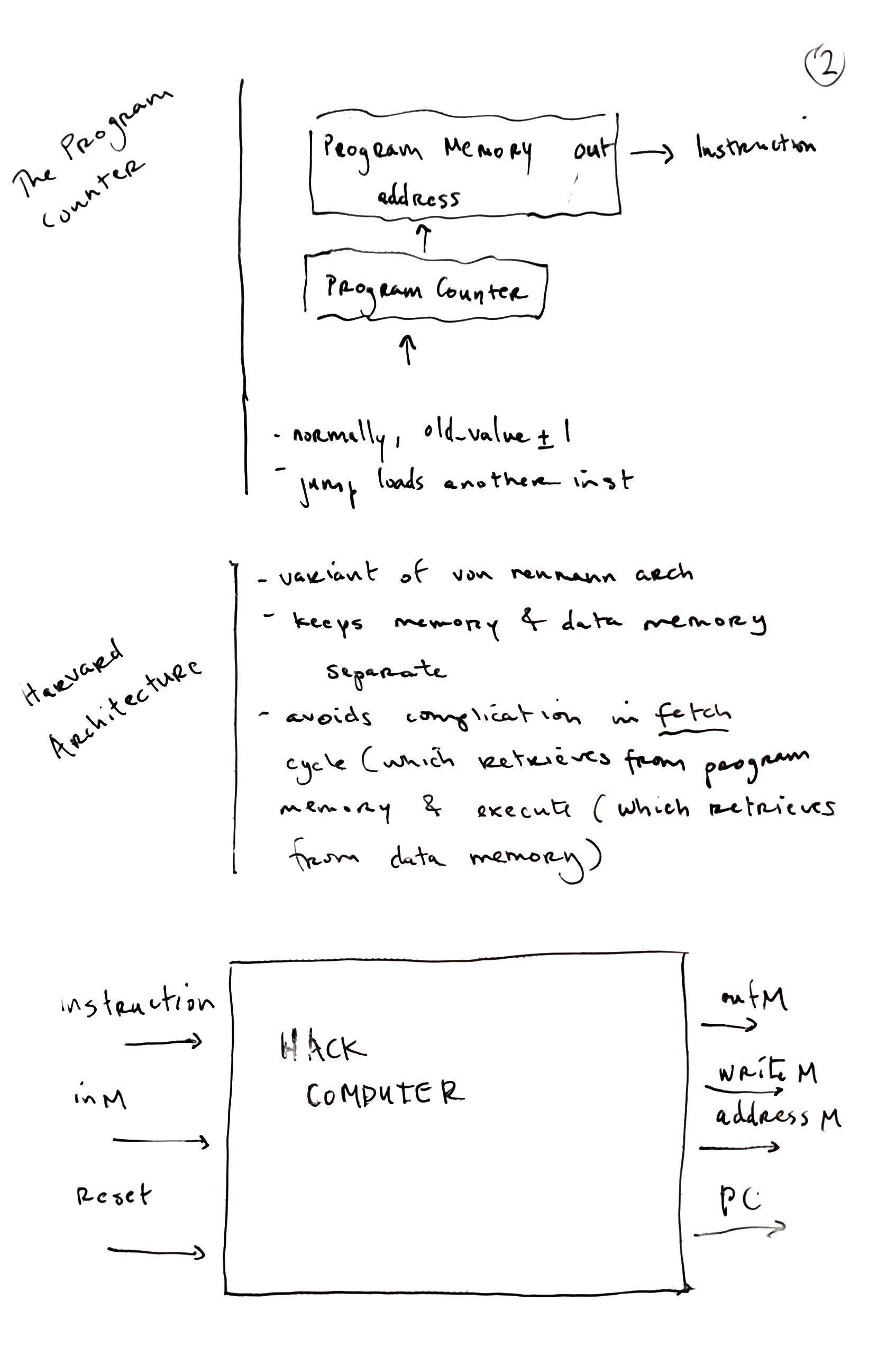
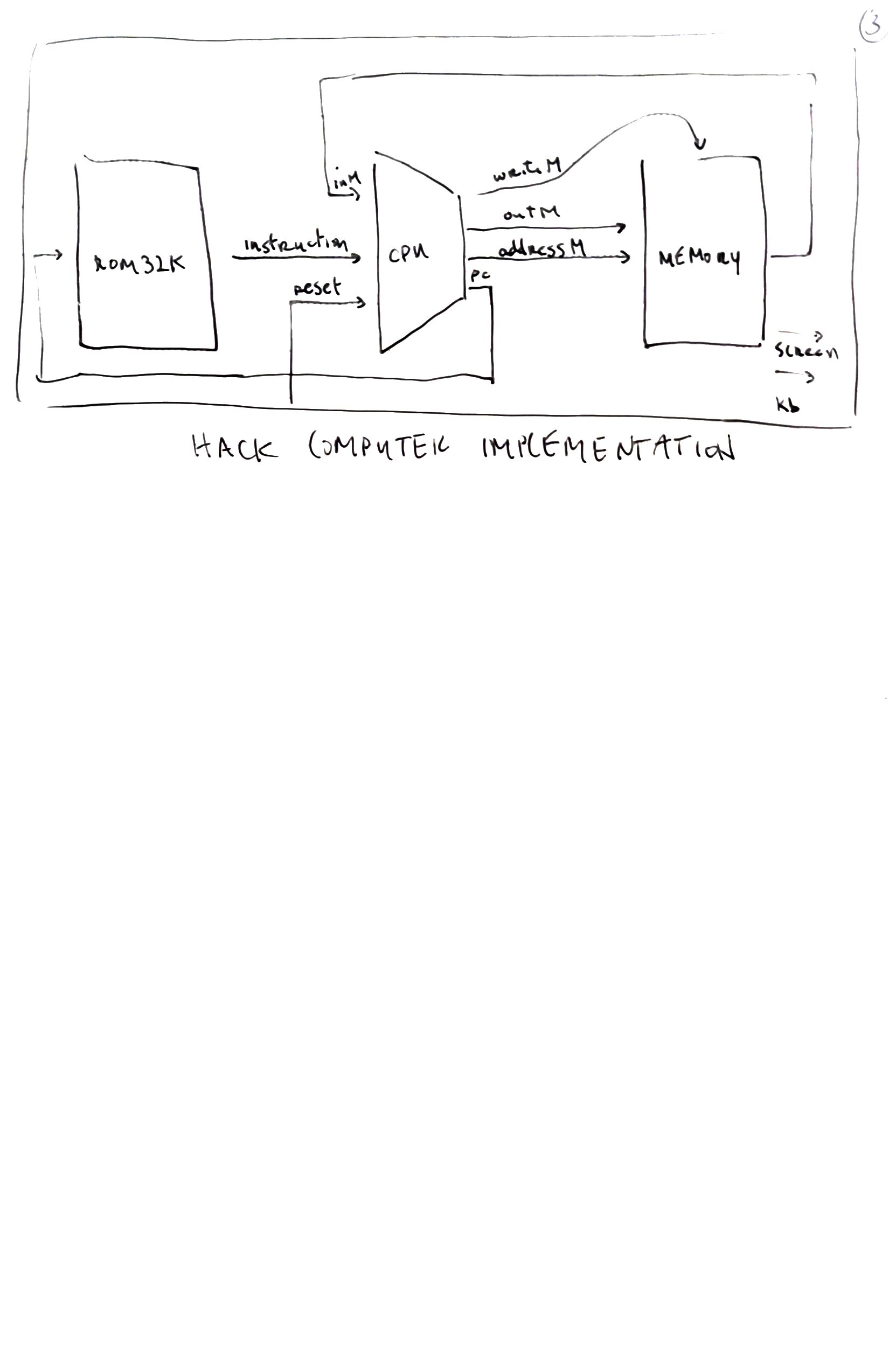
Hardware Description Language

Hardware Simulation

• interactive simulation – active tests
• script-based simulation – pass input and output into simulator

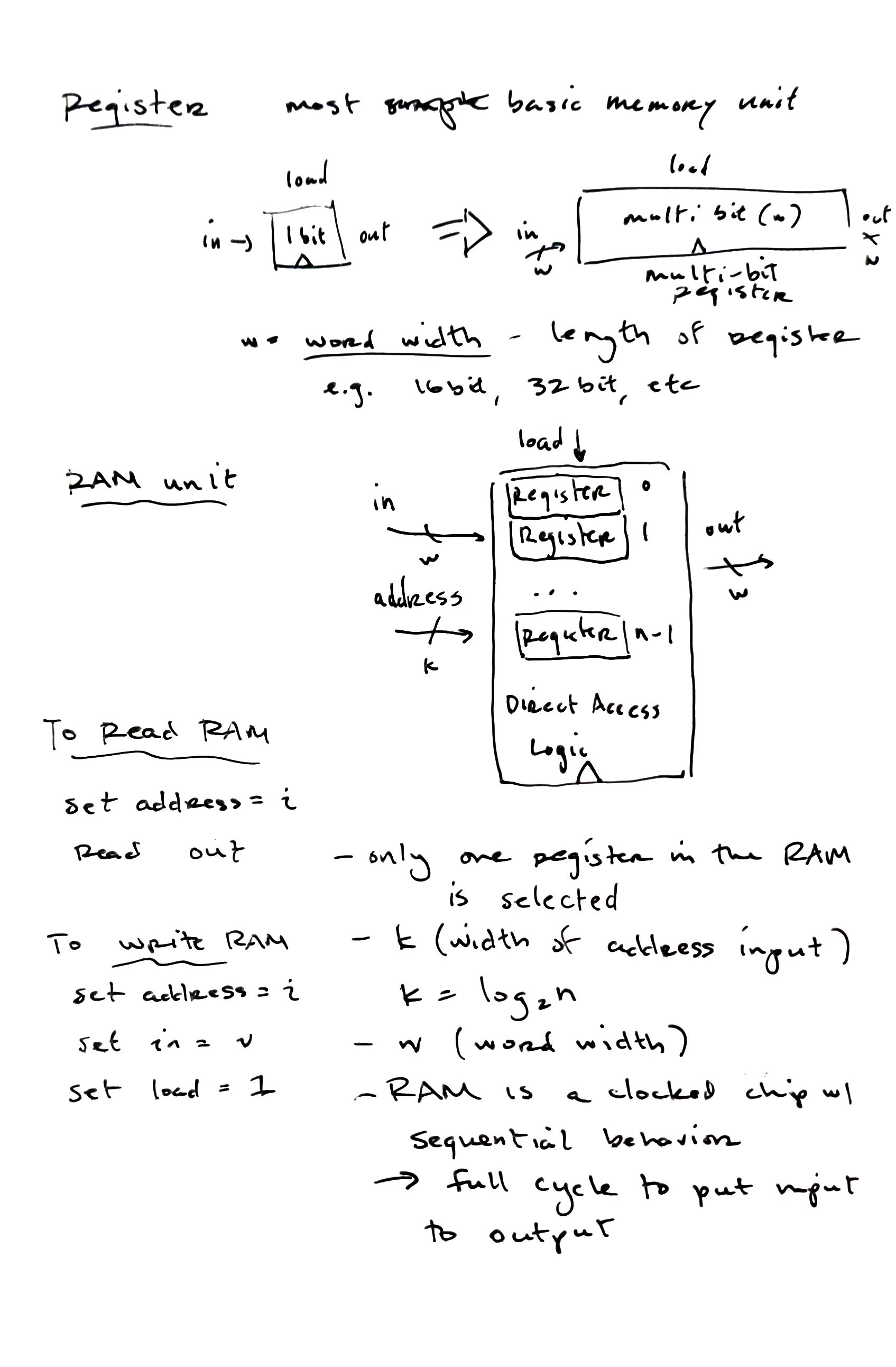
Boolean Arithmetic

convert binary to decimal

1101
2^4 2^3 2^2 2^1
  8   4   2   1
  1   1   0   1
  8 + 4 + 0 + 1
13

convert decimal to binary

99
64 + 32 + 2 + 1
64 32 16 8 4 2 1
1   1  0 0 0 1 1

overflow – if adding numbers that carry over (carry bit), most computers ignore or truncate results

• only need to implement addition and subtraction, can handle multiplication and division in software where it is easier

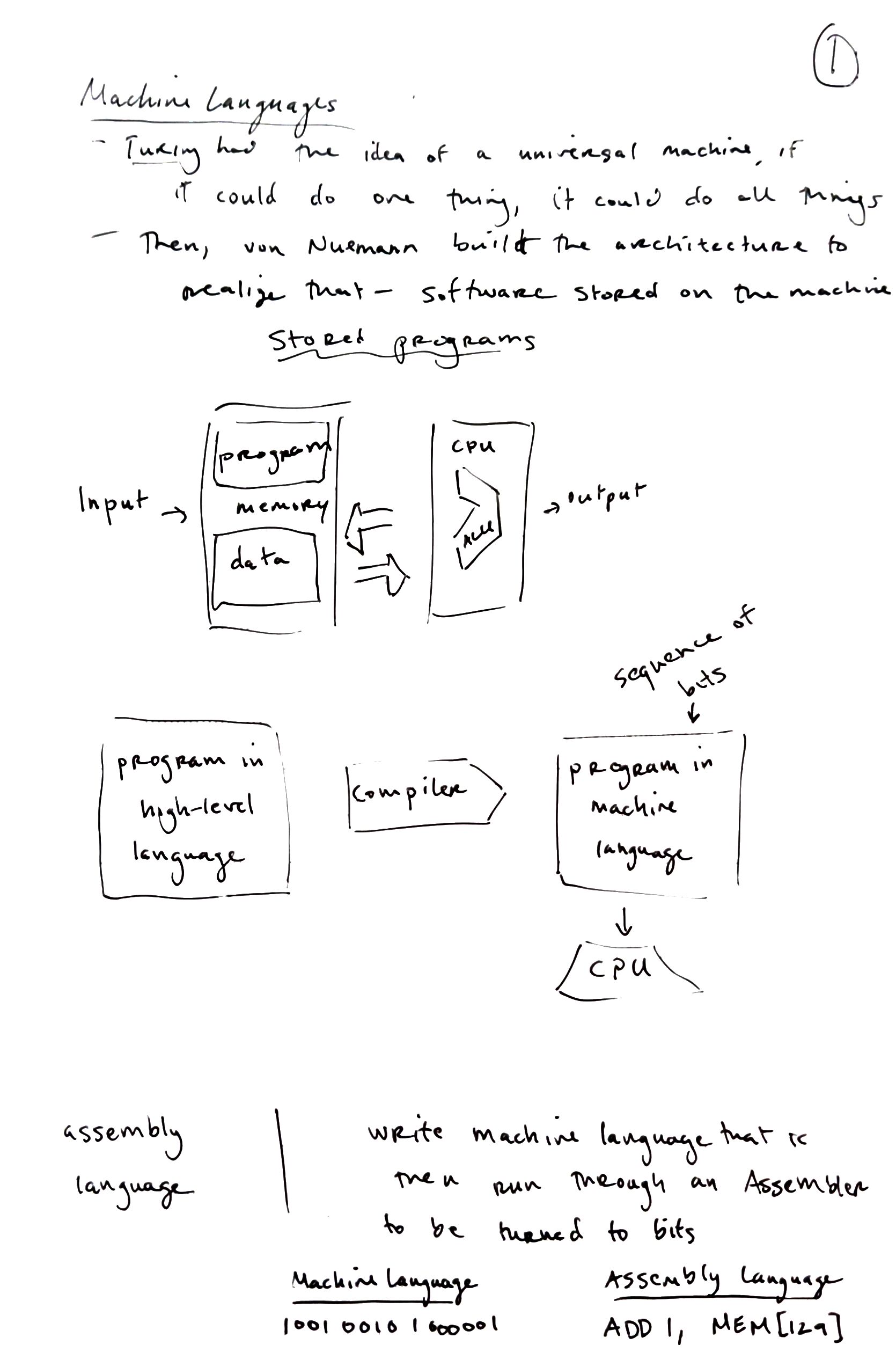
half adder chip

a	b	sum	carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

full adder chip

a	b	c	sum	carry
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

convert to negative, flip bits and add 1

Week 3: Memory

Week 4: Hack Programming